3D Shapes
WALT: Connect three-dimensional objects with their nets and other two-dimensional representations. (ACMMG111)
WILF: We are looking to see if you are able to
WILF: We are looking to see if you are able to
- Identify the properties of a 3D shape.
- Recognise the nets of 3D shapes.
- Work well with others
Pyramids ... Where in the world?
WALT: Recognising pyramids and prisms are found in place other than Egypt
Discovering measurements and cultural significants of pyramids in Asia.
Exploring pyramids
Three-dimensional geometrical shapes occur in nature in crystals of substances. Some of these shapes are commonly used in monuments and sculptures and in the architecture of buildings and other physical structures. Ancient man-made pyramids are found in many parts of the world and in some cases the cultural and archaeological significance of these is still being studied.
Stretching the brain
List where in the world you would find big pyramid-shaped structures.
Pyramids in Asia: There are some significant pyramids in Asia ... even some that are under water!
With your shoulder partner, make a list of pyramid-shaped structures and their country location in Asia.
Choose one Asian pyramid to research in some detail.
Create a poster of that pyramid:
WILF:
- Use of mathematical language to be precise about the shape and nature of the pyramid.
- A net of the pyramid.
- Details about the size of the pyramid compared: Its base measurements and height.
- The age of the pyramid.
- The historical or cultural significance of the pyramid.
Platonic Solids
WALT:
WILF:
- We are going to discover the 5 platonic solids and use Euler's formula in an investigation.
WILF:
- If you can use Euler's formula to identify the 5 platonic solids.
- If you can define the term congruent.
- iValue: I Work well with others.
Defining a platonic solid:
Each one is a congruent polyhedron (a solid with flat faces)
They are special because every face is a regular polygon of the same size and shape. (making them congruent)
Example: each face of the cube is a square.
They are also convex (no "dents" or indentations in them).
They are named after Plato, a famous Greek philosopher and mathematician
Congruent?
Why such a funny word that basically means "equal"? It comes from Latin congruere, "to agree". So the shapes "agree"
Congruent shapes are the same size and shape. If shapes are the same shape but different size, they are called similar.
Each one is a congruent polyhedron (a solid with flat faces)
They are special because every face is a regular polygon of the same size and shape. (making them congruent)
Example: each face of the cube is a square.
They are also convex (no "dents" or indentations in them).
They are named after Plato, a famous Greek philosopher and mathematician
Congruent?
Why such a funny word that basically means "equal"? It comes from Latin congruere, "to agree". So the shapes "agree"
Congruent shapes are the same size and shape. If shapes are the same shape but different size, they are called similar.
Euler's Formula.
Who was Euler?
What is Euler's formula?
Euler has developed a number of different formulas. His most famous is Euler's Identity, which you might like to research on your own.
We are going to be focusing on Euler's formula that is used with 3D shapes.
Euler has developed a number of different formulas. His most famous is Euler's Identity, which you might like to research on your own.
We are going to be focusing on Euler's formula that is used with 3D shapes.
- Number of Faces
- plus the Number of Vertices (corner points)
- minus the Number of Edges
F+V-E=2
Investigation
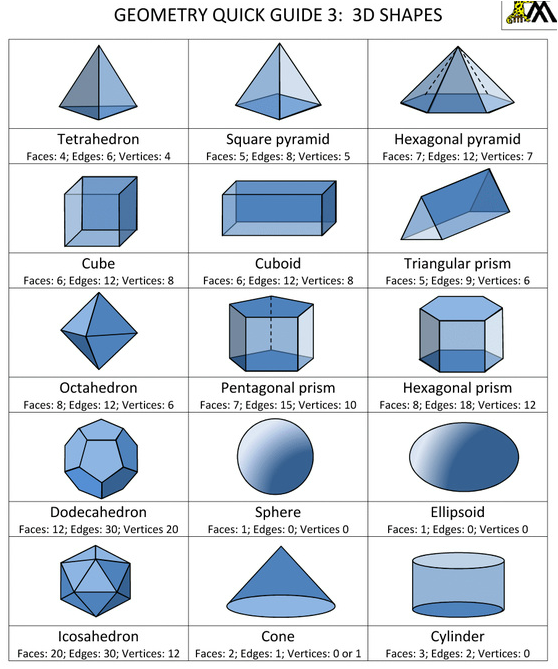
Use Euler's formula to investigate the following shapes. Can you identify which are the 5 Platonic solids?
Use a Venn Diagram to organise your shapes.
Remember the 5 solids have to be:
Use a Venn Diagram to organise your shapes.
Remember the 5 solids have to be:
- Congruent.
- Made up of regular polygons.
- Convex.
- Follow Euler's formula.